flowchart LR
A[PROBLEMA] --> B[Estratégia de Decisão]
B --> C{Solução é BOA?}
7 Uma Introdução à Estatística
Conceitos Inciciais
7.1 Porque Estudar Estatística?
Podemos dizer que a existência da estatística e de outras ciências está conectada a existência de problemas. Não somente a ciência mas o nosso trabalho está conectado a superação de problemas cotidianos. Tomar decisão é o dia a dia do gestor.
Segundo Popper “we study not disciplines, but problems. Often, problems transcend the boundaries of a particular discipline”
A questão central é: Como solucionamos os problemas? Utilizamos a melhor estratégia? A solução foi boa?
7.1.1 Os dois sistemas cognitivos
Os livros abaixo são boas referências sobre a tomada de decisão.
Existem dois sistemas que utilizamos para tomar decisão. O chamado Sistema 1 e o chamado Sistema 2. Segue uma breve descrição de cada um:
Sistema 1:
- Intuitivo, rápido, automático, sem esforço, implícito e emocional
- Pressa,
- Falta de tempo,
- Problemas menos importante
- Mais Falhas/Erros
Sistema 2
- Raciocíonio lento, consciente, esforçado, explícito, lógico
- Requer tempo,
- Mais recursos
- Problemas mais importante
- Menos Falhas
Para o Sistema 1 usamos a nossa intuição que chamamos de Heurística. Vejamos um pouco mais sobre esse sistema.
HEURÍSTICA
São rotinas inconscientes ou atalhos que o nosso cérebro utiliza para lidar com a complexidade.
- Modelo/Regras Intuitivas.
- Próprio do Sistema 1.
- Apesar de processo sofisticado, são passíveis de falhas. Intuição falha
Um Exemplo
Veja a figura abaixo retirada do livro do Bazerman.Responda rápido.
Qual delas tem o tampo mais quadrado?
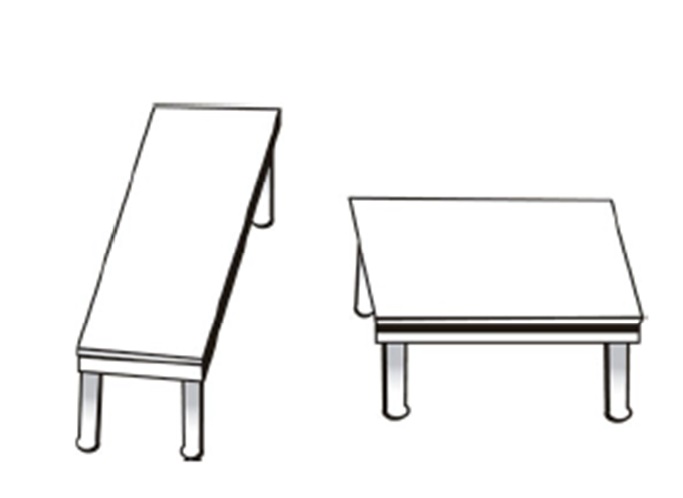
Se você achou que é a segunda mesa, você está alinhado com a grande maioria. Nesse caso você usou o seu sistema 1
Vamos repitir a pergunta:
Qual delas tem o tampo mais quadrado?
Agora use uma régua para medir as mesas. Usamos aqui o sistema 2. Mais tempo e recursos são utlizados. Qual mesa agora você considera mais quadrada? Mudou sua opinião?
Com a régua vemos que as mesas são iguais. Isso mostra que a nossa intuição FALHA.
Tipos de Heurísticas
Heurística da disponibilidade: Usamos o que está mais próximo na memória para calcular a probabilidade.
Heurística da representatividade: Buscamos aquilo que reforça o padrão.
Heurística da hipótese positiva: Assumimos que uma determinada hipótese é verdadeira e não olhamos o contrafactual.
Heurística do afeto: Decisão considera o emocional. Seu humor afetam as decisões.
Para contornar os problemas da intuição e seus viéses na tomada de decisão o primeiro passo é compreender que eles existem e estarmos alerta. E para problemas maiores o uso do sistema 2 torna-se relevante.
Uma das principais ferramentas do sistema 2 é a Estatística. Com os avanços computacionais essa ciência tem se destacado como um dos elementos centrais do data science. Abaixo a figura resume as diversas áreas de desenvolvimento da análise de dados, obviamente não exaustiva:
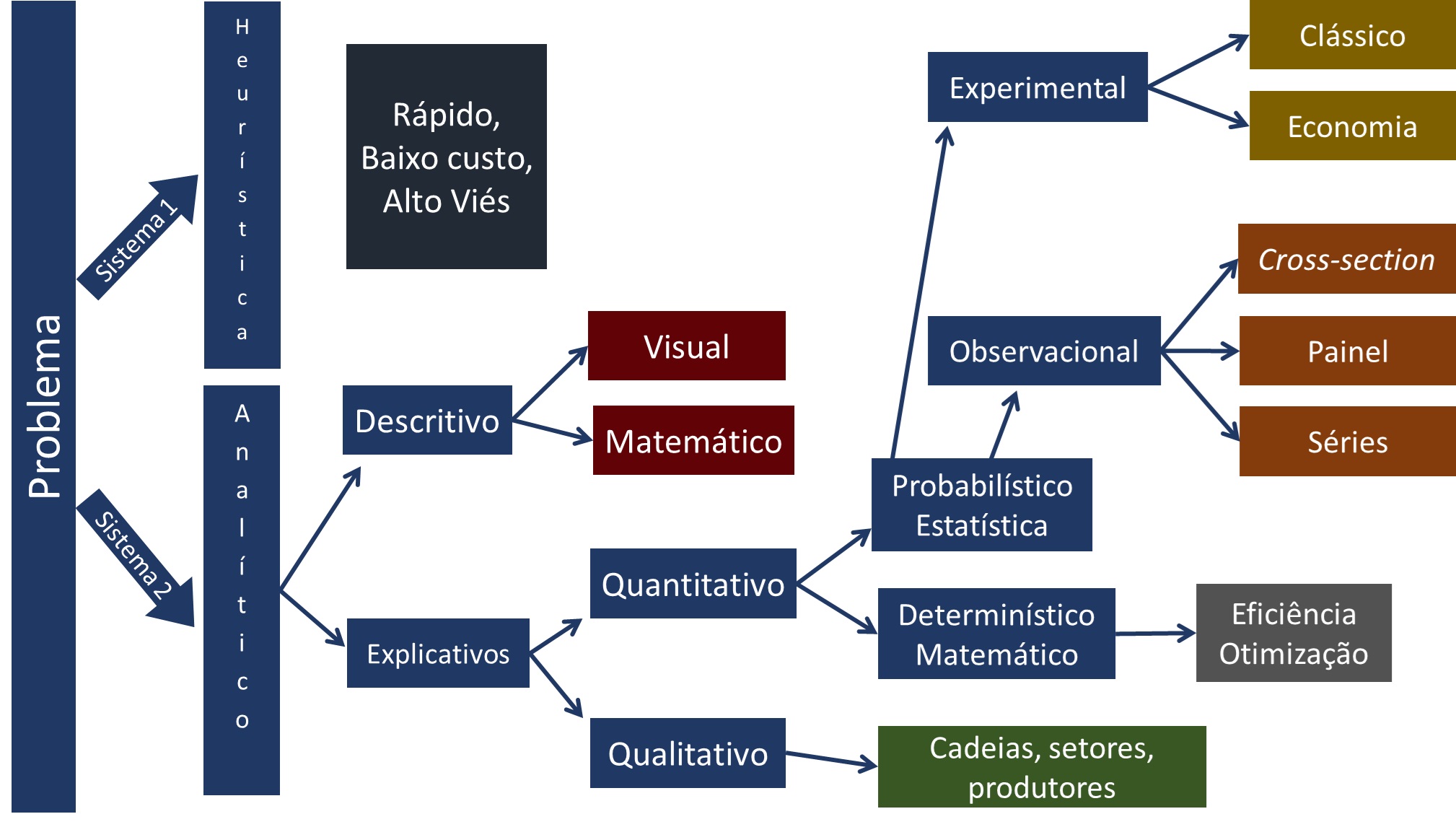
Nosso objetivo é explorar nessa seção a análise descritiva. Chamado hoje no Business Intelligence, que e uma das áreas do Data Science.
7.2 Conceitos Básicos de Estatística
Novamente começamos com um problema e esse definirá a nossa análise. Vejamos alguns problemas que poderiam nos interessar…
O prefeito de Ribeirão Preto vai lançar uma política que fornece vouchers de alimentação para mulheres que estão em situação de pobreza.
Problema: Qual o valor que devo reservar ao programa? Quantas mulheres serão atendidas?
O TJSP vai lançar um programa para reduzir o tempo médio em processos de feminicídio.
Problema: Qual o tempo médio de um processo de feminicídio?
O O governo federal vai lançar um programa para capacitar mulheres que estão fora do mercado de trabalho.
Problema: Quantas mulheres serão alvos dessa política?
7.2.1 A Variável Aleatória
O problema nos define a população que estou interessado. Vamos seguir, a princípio, com o nosso probelma 1 para definirmos alguns conceitos importantes.
No problema 1: me interessa compreender a renda das mulheres que moram em Ribeirão Preto em dado ano. Para ficar simples vamos abreviar o que nos interessa
\[X=\text{Renda das mulheres que moram em Ribeirão Preto em determinado ano}\] Agora posso utilizar o X no lugar do nome. Olhando para a população e pensando que cada nível de renda pode ser representada por uma cor, teremos a seguinte imagem pouco de como a renda se distribui nessa população:

A questão é: quais cores existem e quantas peças de cada cor temos? Para isso usamos um experimento
EXPERIMENTO ALEATÓRIO
O experimento em ciências sociais aplicadas em geral está associada a observação sistemática de pessoas, cidades, empresas ou processos. A ideia é:
- Sortear pessoas e observar a sua caracteristica de forma indefinida e sempre na mesma condição.
- Não consigo dizer o que vai sair no próximo sorteio, apenas consigo descrever os resultados possíveis
- Se repetir o experimento um número grande de vezes uma regularidade aparece.
Se eu conseguir sortear de forma indefinida e na mesma condição as mulheres que moram em Ribeirão Preto e perguntar sobre a sua renda. Eu consigo reorganizar a figura acima da seguinte forma:

ESPAÇO AMOSTRAL
Agora conseguimos organizar os nossos resultados em um lugar chamado espaço amostral. Nele teremos todas as cores (azul, branca, amarela…) que podem acontecer e o número de peças de cada cor (a chance). Em outras palavras teremos todos os possíveis valores de \(X\) e suas probabilidades.
VARIÁVEL ALEATÓRIA
Quanto representamos esse espaço amostral em formato de números é o que chamamos de Variável Aleatória (V.A.). A V.A. é a combinação de tudo que pode acontecer, ou seja, todas as rendas que existem associadas a probabilidade de cada uma das rendas acontecerem.
Existem dois tipos principais de variáveis aleatórias: discretas e contínuas.
VARIÁVEIS ALEATÓRIAS DISCRETAS
É um tipo de variável que conseguimos colocar em lista, seja finita ou infinita \(x_1; x_2;...; x_n;...\) e associa-se a cada um dessses valores uma probabilidade \(p(x_1); p(x_2);...; p(x_n);...\)
Podemos pensar aqui se a pessoa é casada, solteira, divorciada, viúva ou outra condição. Se no processo classificamos como homicídio ou feminicídio, se mora na área urbana ou rural…
Na figura abaixo iremos coletar de 20 processos de homicídio e gostariamos de saber quando é classificado como feminicídio e quanto é classificado como homicídio (p=0,3).
feminicidio <- 0:20
plot(feminicidio,dbinom(feminicidio,size=20,prob=.3),
type='h',
main='Distribuição Binomial (n=20, p=0.3)',
ylab='Probabilidade',
xlab ='Feminicídio',
lwd=3)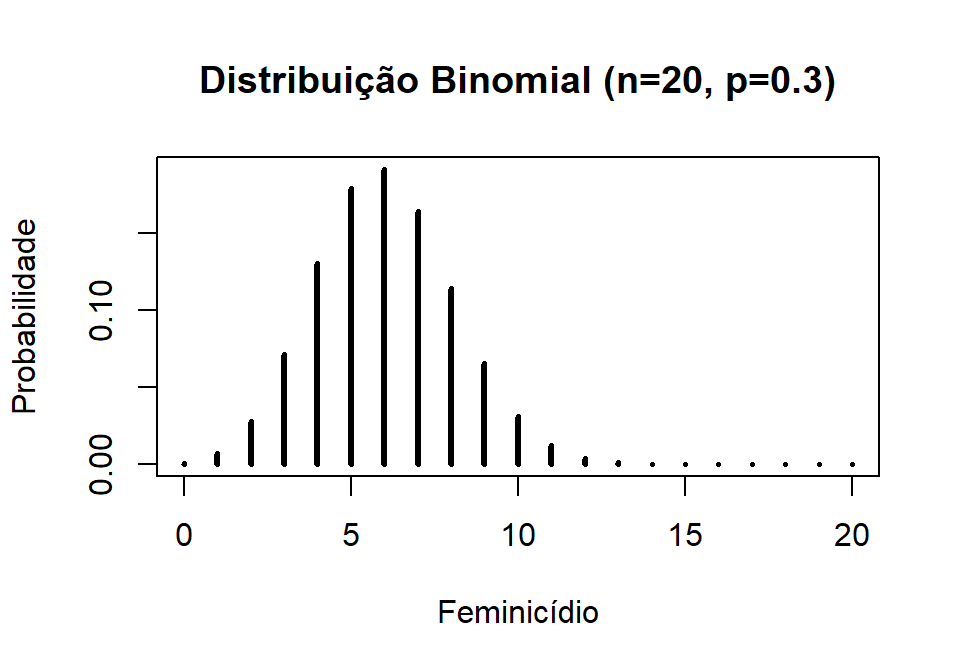
VARIÁVEIS ALEATÓRIAS CONTÍNUAS
Por outro lado, uma variável aleatória contínua pode assumir infinito valores dentro de um intervalo específico. Agora temos infinitas possibilidades de resultados para \(X\) e agora associamos uma função \(f(x)\) que irá descrever o comportamento da probabilidade.
Por exemplo, a altura de uma pessoa, a sua renda, a sua idade, o tempo que demora um processo.
Abaixo temos uma representação de uma distriuição continua da renda das mulheres em Ribeirão Preto, chamada distribuição normal:
rm(list = ls(all.names = TRUE)) #will clear all objects includes hidden objects.
x<-seq(700,1300,1)
fdnorm<-dnorm(x = x, mean = 1000, sd=100)
fdanorm<-pnorm(q = x, mean = 1000, sd=100)
curve(dnorm(x,1000,100),xlim=c(700,1300),main='',xaxt="n",xlab="Renda pc Mulheres", ylab="f(x)",col="darkblue",cex.axis=0.65, cex.lab=0.8)
axis(1,at=c(900, 1000, 1100),labels =
c("-DP(X)","E(x)","DP(x)"),cex.axis=0.65, cex.lab=0.8)
lines(x=c(1000,1000),y=c(0,fdnorm[x==1000]),lty=2, col="black")
lines(x=c(1100,1100),y=c(0,fdnorm[x==1100]),lty=2, col="black")
lines(x=c(900,900),y=c(0,fdnorm[x==900]),lty=2, col="black")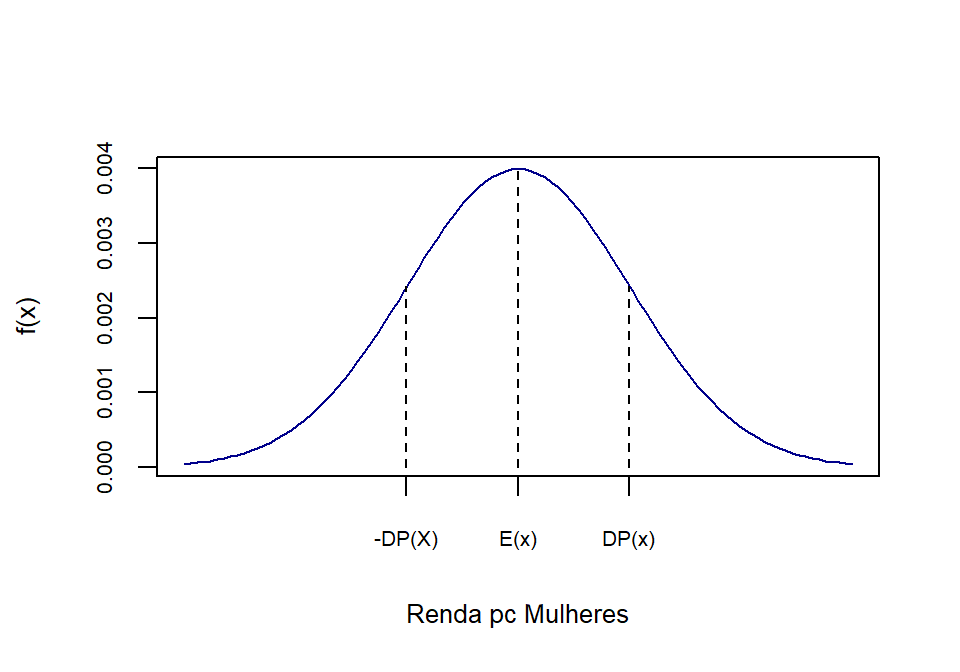
7.2.1.1 Esperança e Variância
O fomato das distribuições vistas dependem principalmente de dois parâmetros: A esperança que é uma medida de centralidade e a variância que é uma medida de dispersão.
ESPERANÇA - \(E(X)\)
É uma medida de centralidade da variável aleatória. É definida como a média ponderada de todos os possíveis resultados de \(X\), onde os pesos são dados pelas probabilidades desses resultados ocorrerem. A esperança de \(X\), \(E(X)\), é calculada como:
\[E(X) = \sum_{x} x \cdot P(X = x)\]
para variáveis discretas.
\[E(X) = \int_{-\infty}^{\infty} x \cdot f(x)\],
para variáveis contínuas
VARIÂNCIA POPULACIONAL - \(Var(X)\)
A variância é uma medida que captura como os dados populacionais se dispersão em relação a sua média (ou esperança).
\[Var(X) =\frac{1}{N} \sum_{1}^{N} (X_i-E(X))^2\] Ou podemos assim representar: \[\text{Var}(X) = E(X^2) - [E(X)]^2\].
DESVIO PADRÃO POPULACIONAL - \(DP(X)\)
A variãncia é uma medida ao quadrado. Se estamos falando da renda seria uma medida da dispersão ao quadrado, ou seja, em \(R\$^{2}\). Para retornar a unidade original usamos o desvio padrão que é:
\[DP(X)=\sqrt{Var(X)}\]
Vejamos o que acontece quando mudamos a esperança e o desvio padrão. No gráfico em azul temos a esperança igual a 10 e devio padrão de 2,5. No gráfico em vermelho temos esperança de 20 e desvio padrão de 10. E no grafico em verde temos esperança de 10 e desvio padrão de 1. Nota-se que quanto menor o desvio padrão mais concentrados são os valores que podem acontecer.
curve(dnorm(x,mean=10,sd=sqrt(2.5)),xlim=c(0,30),ylim=c(0.0,0.4),xaxs="i",yaxs="i",ylab="", col="darkblue")
par(new=T)
curve(dnorm(x,mean=20,sd=sqrt(10)),xlim=c(0,30),ylim=c(0.0,0.4),xaxs="i",yaxs="i",ylab="", col="darkred")
par(new=T)
curve(dnorm(x,mean=20,sd=sqrt(1)),xlim=c(0,30),ylim=c(0.0,0.4),xaxs="i",yaxs="i",ylab="", col="darkgreen") 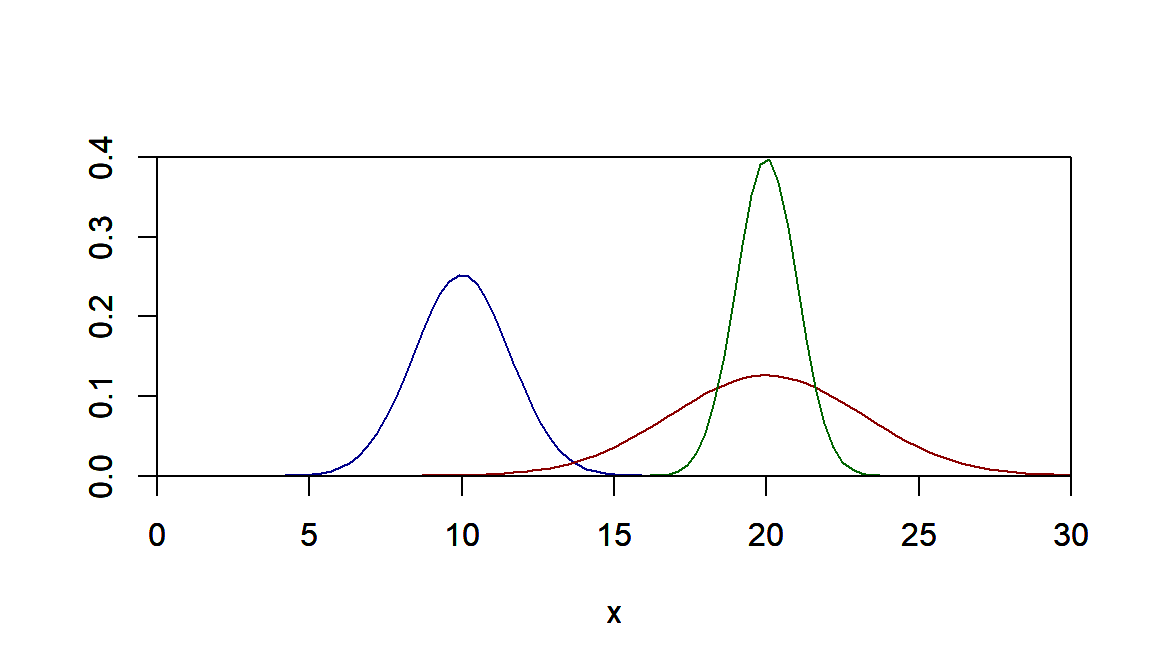
7.2.2 Variáveis Aleatórias Bidimensionais
Muito provavelmente nos interessa observar mais de uma característica de um experimento. Por exemplo, não somente a renda das mulheres em Ribeirão Preto nos interessa, mas o seu consumo alimentar também julgamos importante para o projeto.
Portanto, queremos observar duas características de forma simultânea das mulheres: sua renda e seu consumo alimentar. Ou seja, duas características simultaneamente do mesmo experimento \(\epsilon\) que foi observar as mulheres no município.
Apesar de termos coletados duas informações, temos na realidade três informações. A informação da renda, a informação do consumo alimentar e a informação de como renda e consumo alimentar interagem.
VISUALIZAÇÃO GRÁFICA
Vejamos agora um exemplo de variável aleaória bidimensional:
Normal Bivariada:
Abaixo tem-se uma variável aleatória \((X,Y)\) com distribuição normal bivariada com a esperança de \(X\) igual a 1, de \(Y\) igual a 0, o desvio-padrões iguais a 3 e 2 respectivamente. Aqui consideremaos a correlação de 1 (veremos mais a frente esse conceito)
library(mnormt)
#Para tornar reproduzível
set.seed(0)
#cCriando a normal bivariada
x <- seq(-3, 3, 0.1)
y <- seq(-3, 3, 0.1)
mu <- c(1, 0)
sigma <- matrix(c(3, 1, 1, 2), nrow=2)
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)
#Criando um gráfico de superfície
persp(x, y, z, theta=-30, phi=25, expand=0.6, ticktype='detailed')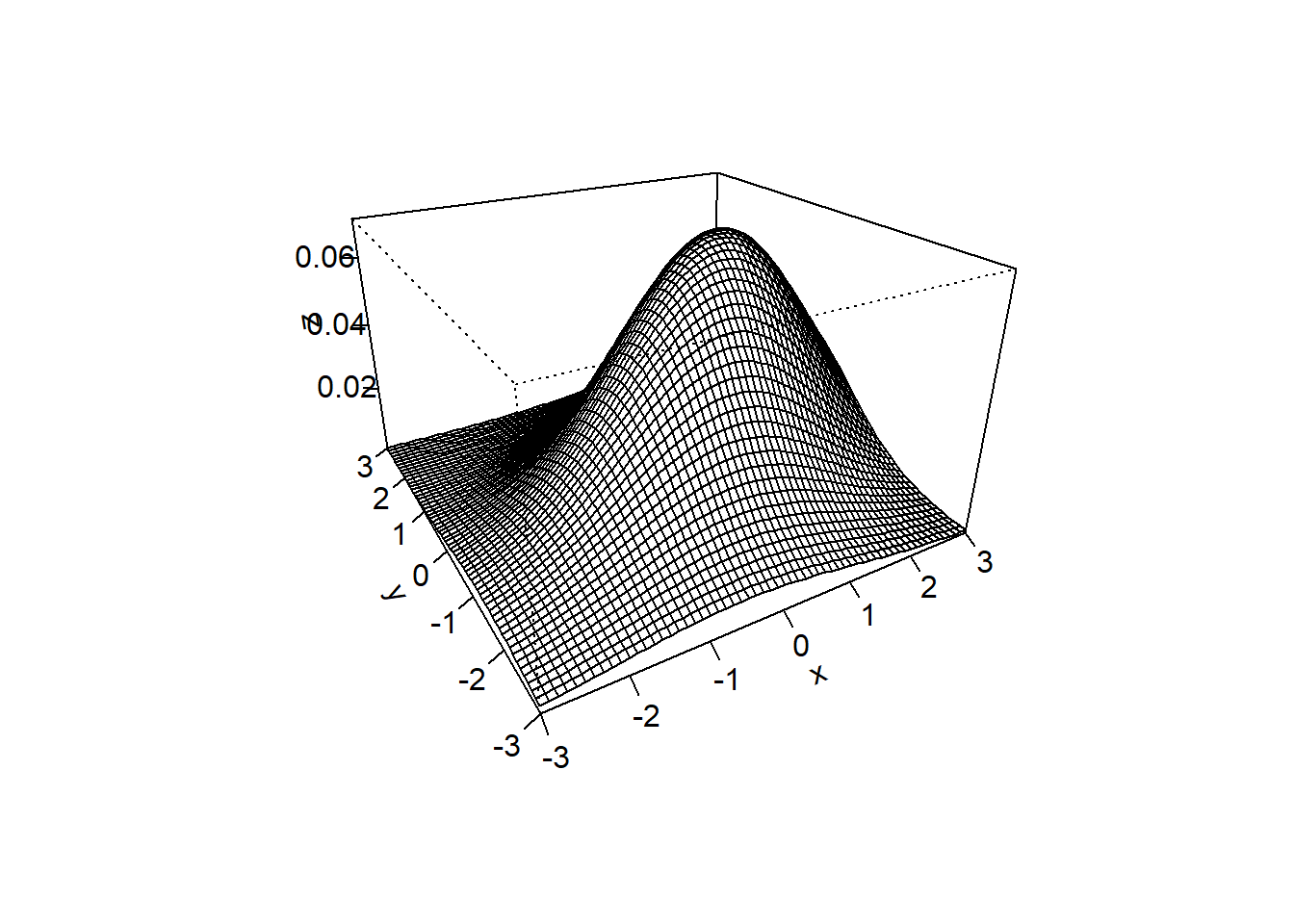
Surge aqui um conceito importante que tenta medir como as características da população se relacionam - uma medida do relacionamento. Assim:
O que acontece com o consumo de alimentos quando a renda das mulheres sobem?
7.2.2.1 Covariância e Correlação
Duas medidas que tentam mensurar o “grau de associação” linear entre X e Y são:
COVARIÂNCIA
\[Cov(X,Y)=E[(X-E(X))(Y-E(Y))]= E(X.Y)-E(X).E(Y)\]
Ela mede a variabilidade conjunta de uma variável aleátoria multidimensional. Como no caso da variância, ela sofre do efeito das escalas de medidas. Para corrigir dividimos pelos desvios padrões. Surge dessa maneira a medida de correlação.
CORRELAÇÃO
\[\rho_{X,Y}=\frac{E[(X-E(X))(Y-E(Y))]}{\sqrt{Var(X)Var(Y)}}=\frac{Cov(X,Y)}{DP(X).DP(Y)}\]
A correlação mede o GRAU DE ASSOCIAÇÃO LINEAR. Associações não lineares não são capturadas pela correlação.
A correlação \(\rho_{X,Y}\) varia de -1 até 1. Sendo que:
\(\rho\) próximo a 1 e -1 indicam alto grau de linearidade e \(\rho\) próximo a 0 indica ausência de relação linear - mas não diz nada sobre relações não-lineares.
VISUALIZAÇÃO GRÁFICA
Veja no gráfico abaixo que a variável 4 e 5 possuem correlação perfeita, igual a -1. E as variáveis 3 e 1 não possuem grau de associação linear, correlação próxima a 0.
Warning: pacote 'psych' foi compilado no R versão 4.4.1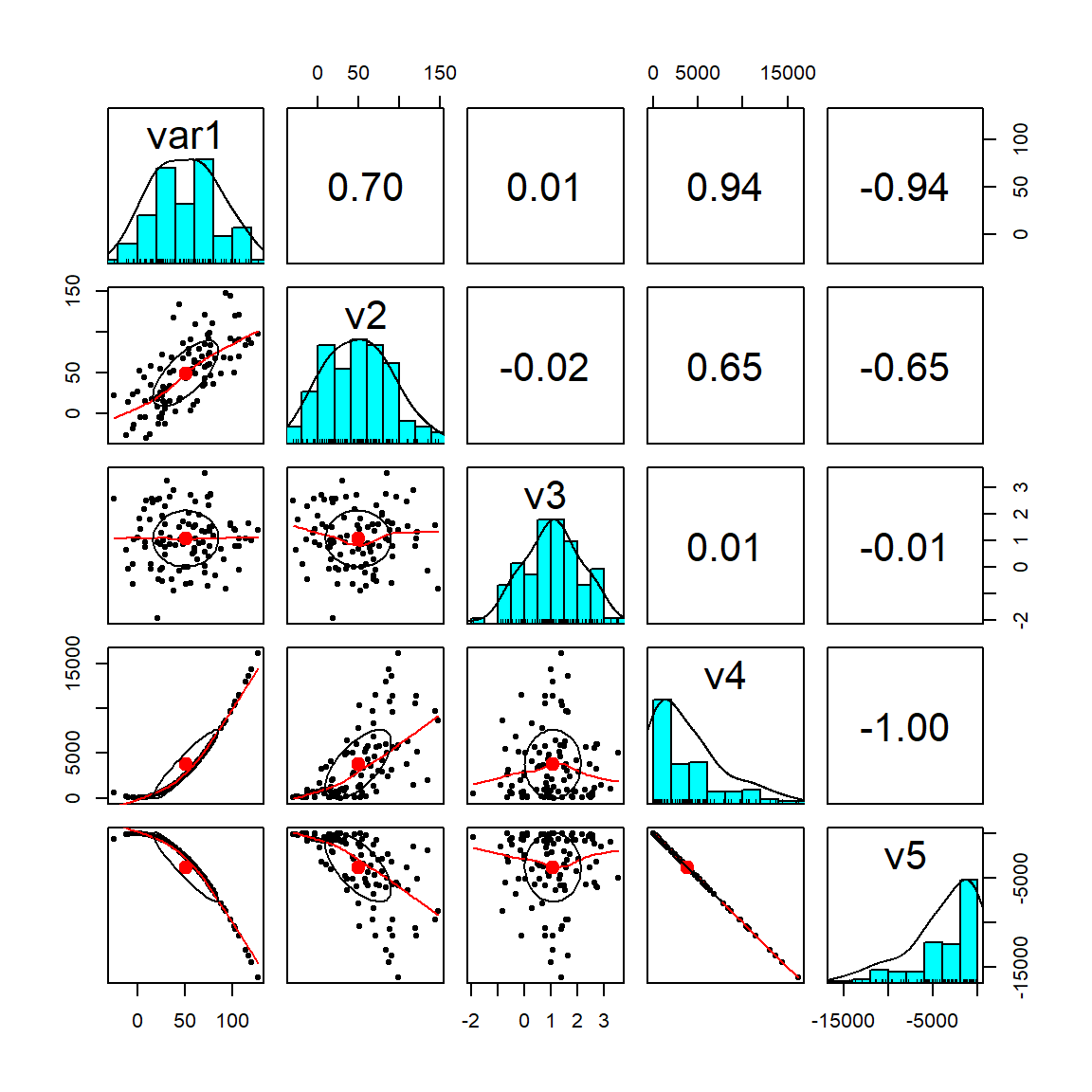
7.3 Conceitos Básicos Inferência Estatística
Dado a nossa pergunta ou problema, gostariamos de saber as carcateística de uma população.
Entretantom um processo de levantamento de informações é em geral caro e em muitas situações é destrutivo. Em ciências sociais estamos interessados em características de pessoas, empresas, municípios, estados, países etc. Não é destrutivo mas é uma coleta cara. Por exemplo, o Censo demográfico de 2010 custou R$ 1,3 bilhões, ou aproximadamente R$ 2,2 bi em reais de 2020. O valor é de aproximadamente R$ 35,00 por domicílio.
Dessa forma nosso objetivo aqui é:
A partir de uma amostra da população realizar inferência sobre toda a população
7.3.1 Exemplos do príncipio no dia a dia
Pense nessas situações:
- Para medir a glicose muitos pacientes usam uma gota de sangue e um pequeno aparelho. A partir dele sabem quanto tem no corpo todo, basta uma gota para termos boa certeza de quanto é taxa de glicose!
- Para saber se a quantidade de sal está adequada em uma grande panela de arroz, basta uma pequena colher de chá para termos uma boa certeza!
- Abacaxis às vezes são vendidos em caminhões na rua. Quando paramos provamos e são doces. Compramos 4 por 10. Qual a certeza que esses que vc está levando estejam também doces? É diferente das situações anteriores?
Com certeza vc deve ter pensado que essas situações tem grau de certeza variáveis. A diferença está em quão homogênea é a característica na população, o sal no arroz e a glicose no sangue devem ser muito bem distribuidas, ou seja, bem homogêneas. Já a doçura no abacaxi deve ter distribuição maior e provar apenas um abacaxi não nos dá uma ideia do todo.
Esse é um erro muito comum, a partir de uma ou poucas observações dizer que o todo se comporta da mesma maneira, esse erro se agrava quando maior é a heterogeneidade!!!
7.3.2 População, Amostra, Parâmetros e Estimadores
7.3.3 População e amostra
flowchart LR A[POPULAÇÃO] --> B[Totalidade das observações sob Investigação] A --> C[AMOSTRA] C --> D[Subconjunto da População]
A definição da população depende da pergunta de pesquisa ou análise. Se queremos saber qual o salário médio dos empregados do setor industrial no estado de São Paulo para determinado ano, nossa população são todos os funcionários das indústrias instaladas no estado de São Paulo para esse ano. Se queremos os determinantes do desempenho escolar dos alunos do ensino fundamental no Brasil em 2019, nossa população será esse grupo de alunos nesse ano. Se quisermos avaliar o gasto municipal no ano anterior as eleições no Brasil, temos nossa população formada pelos municípios para o ano de análise.
Quem define a população é o objetivo do seu trabalho!! Ou seja, seu problema de pesquisa
7.3.4 Amostragem Aleatória Simples
Existem várias maneiras de fazer uma análise aleatória, uma delas é a simples. Vejamos primeiro um processo de amostragem não aleatório e que possui tendenciosidade. A figura abaixo mostra esse processo[^7]:
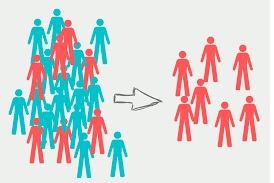
Observa-se que existe uma supervalorização do vermelho e uma subvalorização do azul. Chegariamos a conclusão, caso isso fosse uma pesquisa eleitoral, que o candidato vermelho, segunda amostra teria mais chance de ganhar e o azul quase nenhuma chance. O que não condiz com a população. Dizemos que temos uma amostra viesada ou tendenciosa.
Um processo de amostragem aleatório requer que as características presentes na população estejam presentes na amostras e estejam balanceadas, ou seja, que a sua leitura represente bem o todo.
7.4 Estatística e Parâmetro
flowchart LR A[PARÂMETRO] --> B[Medida que descreve uma característica da população]
Os parâmetros definem as características de uma população. Qual a renda média da população, qual o desemprego médio da população, qual o desempenho médio educacional, qual a expectativa de vida média na população etc. São características que em geral não observamos.
Uma pergunta, qual o tempo médio que demora um processo de feminicídio? Perceba que mesmo características da população que conhecemos são de difíceis de conhecermos. Temos que nos valer de uma parte e tentar estimar o que seriam os valores dessas características.
flowchart LR A[ESTATÍSTICA] --> B[Medida que descreve uma característica da amostra]
Sejam \(x_1, x_2,..., x_{n}\) os valores medidos a cada para cada medição de \(X\). Podemos definir uma estatística como:
\[ t= H (x_1, x_2, ..., x_{n})\]
Alguns exemplos de T:
\[ \text{Média}: \ \overline{x}=\frac{\sum_{i=1}^{n} x_i}{n}\]
\[ \text{Variância:} \ s^{2}= \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \overline{x})^{2} \]
\[ x_{(1)}: Min\{x_1, ..., x_n\}\]
Vejamos a tabela abaixo que já faz uma primeira associação entre estatística e parâmetro:
| Parâmetro | Estatística | ||
|---|---|---|---|
| Esperança | \(E(X)=\mu\) | \(\bar{X}\) | Média |
| Variância Pop. | \(Var(X)=\sigma^2\) | \(S^2;\sigma^2\) | Variância Amostral |
| Mediana Pop. | Md | md | Mediana Amostral |
| Proporção Pop. | p | \(\hat{p}\) | Proporção Amostral |
Tabela 1 - Parâmetros populacionais e as Estatísticas associadas
Como regra geral, os parâmetros são representados por letras gregas e as estatística com letras do nosso alfabeto (latino) ou letra grega com com chapéu para indicar que é uma estatística.
ESTIMADORES Um estimador é uma estatística calculada a partir da amostra que é usada para estimar um parâmetro desconhecido da população. Nos permitem fazer inferências sobre os parâmetros com base nos dados amostrais. Por exemplo, a média amostral é um estimador da média populacional, e a proporção amostral é um estimador da proporção populacional.
7.5 Teste de Hipotese (Parâmetros).
Algumas vezes gostariamos de testar se uma teoria é verossímil com a realidade ou mesmo testar teorias diferentes e verificar qual seria a mais plausível com base na realidade.
Dessa forma, gostariamos de testar se uma sobre a população é mais plausível, ou seja, se os dados amostrais trazem evidências que apoiam ou não essa hipótese. Por exemplo:
- Verificar se um determinado medicamento não tem efeito sobre a mortalidade causada por um determinado virus ou se possui efeito.
- Verificar se a quantidade de gordura anunciado pelo fabricante de um produto realmente está correta ou é maior.
- Se a afirmativa de um canditado de que possui a maioria dos votos é verdadeira ou é menor.
- Verificar se as rendas entre duas comunidades são as mesmas para podermos lançar uma política de apoio
- Verifcar se uma política do aumento do recurso as empresas não afeta falência ou se tem efeito.
- se o tempo médio de encaminhamento e deferimento de medida protetiva de urgência é menor do que 48 horas em casos de violência doméstica e familiar contra a mulher.
Aqui faremos algo muito parecido a presunção de inocência, assumimos que a pessoa ou empresa é “inocente”.
- O medicamento não tem efeito,
- O teor de gordura está certo,
- O candidato tem maioria,
- As comunidades possuem a mesma renda,
- O recurso financeiro não afeta o número de falências
- O deferimento ocorre em até 48h.
Partimos da premissa de que a hipótese inicial é a correta e tentamos verificar com os fatos (dados amostrais) se essa hipótese colocada é verossímil.
7.5.1 Construíndo a Hipótese Nula
Imaginemos o seguinte caso. Um estudo sobre a eficiência do Judiciário sugere que a duração média de um determinado tipo de processo na Justiça Federal é de 600 dias. No entanto, advogados e operadores do direito argumentam que, na prática, esse tempo pode ser maior devido a atrasos processuais e recursos frequentes. A questão é: a estimativa oficial está correta ou os operadores do direito têm razão?
Dessa forma, temos duas hipóteses distintas:
- A primeira afirma que o tempo médio de duração do processo, \(\mu\), é de 600 dias,
- A segunda sugere que a duração real é superior a 600 dias.
Vamos assumir que a estimativa oficial está correta até que se prove o contrário, e chamaremos essa afirmativa de hipótese nula (\(H_0\)):
\[H_0: \quad \mu = 600 \text{ dias}\]
Já a hipótese alternativa (\(H_1\)), que representa a teoria concorrente dos operadores do direito, sugere que a média real de duração do processo é maior:
\[ H_1: \quad \mu > 600 \text{ dias}\]
Nosso problema, então, é decidir se devemos aceitar ou rejeitar a hipótese nula \(H_0\) — de que o tempo médio é de 600 dias — em favor da hipótese alternativa \(H_1\), que afirma que os processos, na realidade, levam mais tempo para serem concluídos.
Juntas:
\[H_0: \quad \mu = 600\] \[H_1: \quad \mu > 600\]
Esse modelo pode ser aplicado utilizando dados reais de processos judiciais para verificar se a alegação dos operadores do direito se sustenta estatisticamente.
7.5.2 O Teste Estatístico
Qual dessas duas hipóteses é mais plausível?
Para isso devemos nos valer de um processo de amostragem, onde faremos \(n\) medições do tempo médio dos processos (que chamaremos de X), \(X_1, X_2, ..., X_n\), e obteremos os valores em dias do tempo médio de cada processo amostrado \(x_1, x_2,...x_n\).
Com base na amostra devemos realizar algum tipo de cálculo que nos permite inferir se rejeitamos ou não \(H_0\), se é plausível ou não a hipótese colocada. Isso é o que chamamos de teste estatístico:
\[T = h(X_1,X_2, . . .,X_n)\]
Decidindo qual o \(T\) utilizar - a função \(h\) que será aplicado aos valores da amostra - devemos compreender qual é a distribuição dessa estatística sob a condição de que a hipótese \(H_0\) for a verdadeira.
Queremos aqui saber se a amostra tivesse sido extraída de contratos com esperança do tempo de duração , \(\mathbb{E(X)}\), de 600 dias, quais seriam os valores típicos para a distribuição do estimador T? Dessa forma, podemos comparar esses valores típicos com o que obtivemos no processo de amostragem.
Vejamos no nosso exemplo, gostariamos de verificar a hipótese de que a esperança do tempo médio, \(\mu\) é de 600 dias. Como já vimos uma boa alternativa de teste estatístico poderia ser a média, \(\bar{X}\). Assim o teste estatístico seria:
\[\bar{X} = \frac{\sum_i^n(X_i)}{n}\]
Com base na amostra observada \(x_1, x_2, ..., x_3\) poderiamos obter a estimativa do tempo médio, ou seja, \(\bar{x}\). Como saber se essa média calculada nos traz mais evidência a favor de \(H_0\) ou \(H_1\)? Veja a Figura abaixo para pensarmos no problema.
A figura considera o estimador \(\bar{X}\). A esquerda temos os valores do estimador que atestam que a hipótese \(H_0\) é a mais plausível, quando mais próxima a estimativa de 600 maior evidência que \(H_0\) é verdadeira. Ao caminhar para a direita, os valores do estimador se distanciam de 600, e mais evidência de que \(H_0\) não é plausível.
Dessa forma, precisamos de um ponto no qual (interrogação na figura) onde valores menores do estimador são favoráveis a hipótese nula e valores maiores são mais favoráveis a hipótese alternativa. Por exemplo, se no nosso processo de amostragem obtivemos a estimativa de \(\bar{x}=700\), isso é mais favorável a \(H_0\) ou \(H_1\)?
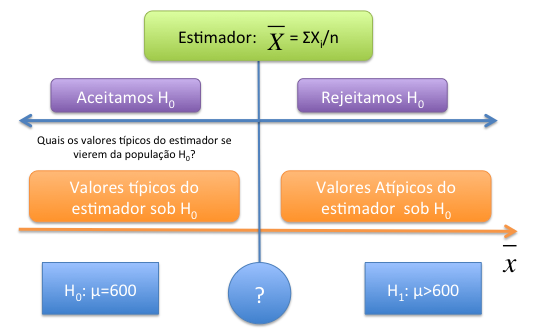
Para saber qual seriam os valores típicos do estimador \(\bar{X}\) sob \(H_0\) imagine que a população \(X\) seja \(N(600,100^2)\), ou seja, tem esperança 600 e desvio padrão populacional de 100. Essa é a afirmação da Justiça Federal, ou seja, nosso \(H_0\).
Já sabemos que um processo de amostragem cada uma das \(n\) medições \(X_1, X_2, ...,X_n\) possuem a mesma distribuição de \(X\). E também sabemos por definição que o estimador \(\bar{X}\) terá uma distribuição:
\[N(600,\frac{100^2}{n})\].
Supondo que retiramos uma amostra de 25 processos, logo os valores típicos do estimador sob \(H_0\) são \(N(600,\frac{100^2}{25})\). Vejamos abaixo a simulação do estimador \(\bar{X}\), os valores típicos para esse caso, e onde se encontra o valor de 700.
x<-seq(500,700,0.1)
fdnorm<-dnorm(x = x, mean = 600, sd=20)
regiao=seq(560,640,0.01)
cord.x <- c(min(regiao),regiao,max(regiao))
cord.y <- c(0,dnorm(regiao,mean=600, sd=20),0)
curve(dnorm(x,600,20),xlim=c(500,700),xlab=expression(bar(x)),type="l",
col="steelblue4",lwd=2, ylab=expression(paste("f(", bar(x),
")")),xaxt="n",cex.axis=0.65, cex.lab=0.8 )
axis(1,at=c(500,540,560,580, 600, 620, 640,660, 700),labels =
c(500,540,560,580, 600, 620, 640,660, 700),cex.axis=0.7, cex.lab=0.8)
polygon(cord.x,cord.y,col='lightgray')
abline(v=600, col="steelblue4", lty=2, lwd=2)
text(602, 0.001, expression(mu))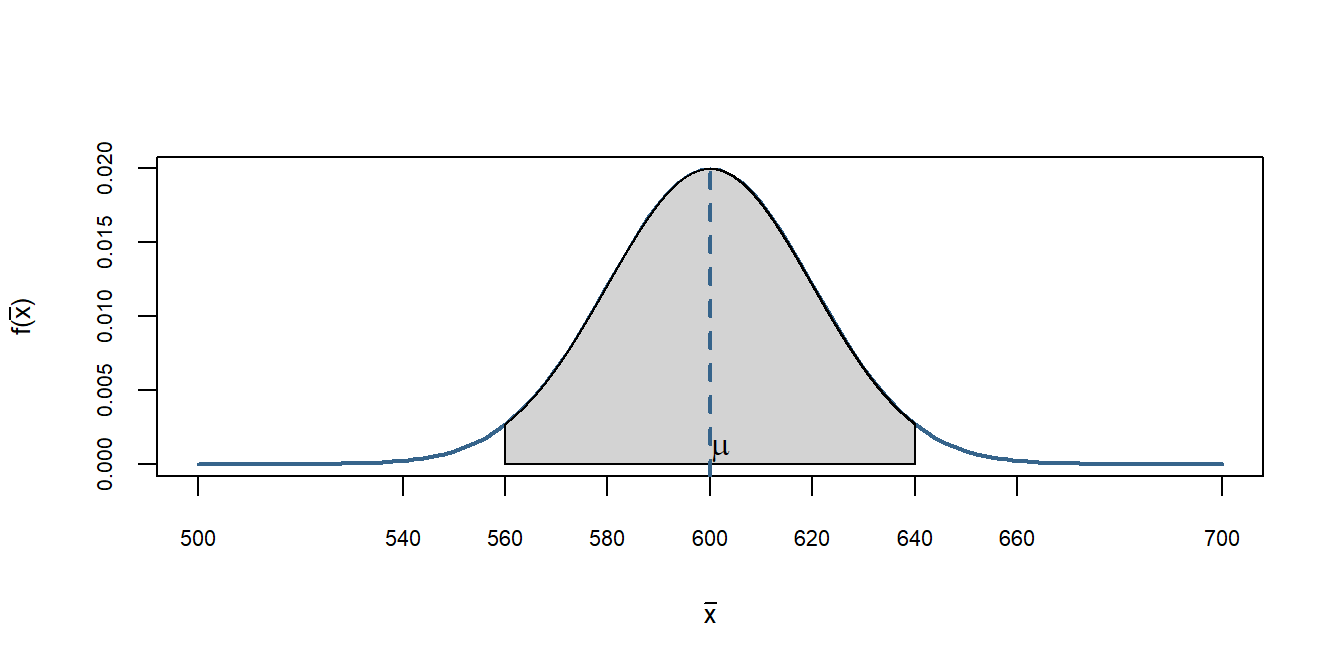
No centro temos a \(E(\bar{X})=\mu=600\). Observamos que para o tamanho amostral que retiramos e sob \(H_0\) os valores típicos oscilam mais ou menos entre 560 e 640 - dois desvios padrão para cima e para baixo (lembrem-se que nesse intervalo temos mais de 95% das observaçoes).
Quanto retiramos a amostra e calculamos o valor da média obtivemos \(\bar{x}=700\). Observe no gráfico acima onde está o valor de 700, muita a frente e notamos claramente que a probabilidade de obtermos esse valor de média com uma amostra retirada da população \(N(600,100^2)\), é praticamente 0.
Portanto, existem evidências de que essa amostra não veio de uma população conforme descrita pela Justiça Federal e sim de processos com tempo médio (esperança) maior do que 600. Portanto, dizemos que rejeitamos \(H_0\).
7.5.3 Erro Tipo I (EI) e Erro Tipo II (EII)
Aqui precisamos distinguir duas ideias, a primeiro é a existência da verdadeira população e a segunda é o que achamos ser a verdadeira população com base na análise que fizemos. Aqui surge o que chamamos de erro estatístico. Não temos como fugir dele, somente controlá-lo. Vejamos a tabela abaixo que resume as possibilidades:
| A Decisão | (\(H_0\)) é verdadeiro | (\(H_1\)) é verdadeiro |
|---|---|---|
| Rejeitar (\(H_0\)) | Erro Tipo I (EI) | Correto |
| Não Rejeitar (\(H_0\)) | Correto | Erro Tipo II (EII) |
Observe que a nossa decisão pode incorrer em dois erros diversos.
Erro Tipo I e Erro Tipo II
Erro Tipo I (EI): ocorre quando “indevidamente” rejeitamemos \(H_0\). Nesse caso \(H_0\) era verdadeira e rejeitamos.\
Erro Tipo II (EII): ocorre quando “indevidamente” não rejeitamos \(H_0\). Nesse caso não rejeitamos \(H_0\) e na verdade \(H_1\) é verdadeira.
O primeiro erro é o chamado na literatura médica de falso negativo, ou seja, classifica a pessoa não portadora da doença (negativa) e na verdade ela possui.
O segundo tipo é o falso positivo, onde classifica-se a pessoa com a doença quando na realidade ela não possui.
Nosso desafio agora é estabelecer um critério de decisão, o ponto a partir do qual dizemos que \(H_0\) não parece mais provável (Figura Teste de Hipótese - Intuição). Essa chamaremos de região crítica ou de rejeição.
- EI \((\alpha)\)- Dizer que o tempo médio é maior que 600, quando na realizadade ela é de 600.
- EII \((\beta)\)- Dizer que tempo médio é de 600 quando na realidade ela é maior do que 600.
Vamos retomar o nosso exemplo. Foi retirada uma amostra de \(n=25\) processos e por definição a distribuição de \(\bar{X}\) sob \(H_0\) será \(N(600,\frac{100^2}{25})\). A hipótese a ser testada será:
\[H_0: \qquad \mu=600\] \[H_1: \qquad \mu>600\]
Uma maneira de acharmos o valor a partir do qual teremos a região crítica ou de rejeição, seria controlar o Erro Tipo I \((\alpha)\). Podemos dizer que gostariamos de cometer o Erro Tipo I em apenas 5% dos casos.
A chance de retirarmos um amostra e o valor da estimativa ser maior que o valor de decisão é de 5% dos casos, os outros 95% sempre cairão na área de aceitação.
\[P(Z_{\bar{X}} \geq z_c|H_0)=0.05= \alpha\] Olhando a tabela temos:
\[P(Z_{\bar{X}} \geq 1.65|H_0)=0.05= \alpha\] \[z_c =\frac{\bar{X}+600}{100/5}\] \[1.65 = \frac{\bar{X}+600}{20}\] \[\bar{X}=600+1.65*20=633\]
Portanto,
\[P(\bar{X}\geq 633|H_0)=0.05= \alpha\]
Logo, temos agora uma regra de decisão que tenta controlar o Erro Tipo I. A nossa regra de decisão agora é rejeitar \(H_0\) toda vez que o valor calculado da estimativa de \(\bar{X}\) for maior do que 633 e aceitar quando for menor. Assim nossa região crítica será:
\[RC =\{\bar{x} \in \mathbb{R} | \bar{x} \geq 633\}\]
Isso implica que a probabilidade de rejeitarmos \(H_0\) (de que o tempomédio não é de 600), e na verdade ela ser de 600 é de 5%.
Vejamos o gráfico:
x<-seq(500,700,0.1)
fdnorm<-dnorm(x = x, mean = 600, sd=20)
fdnorm1<-dnorm(x = x, mean = 660, sd=20)
regiao=seq(633,700,0.01)
cord.x <- c(min(regiao),regiao,max(regiao))
cord.y <- c(0,dnorm(regiao,mean=600, sd=20),0)
curve(dnorm(x,600,20),xlim=c(500,700),xlab=expression(bar(x)),type="l",
col="steelblue4",lwd=2, ylab=expression(paste("f(", bar(x),
")")),xaxt="n",cex.axis=0.65, cex.lab=0.8 )
axis(1,at=c(500,540,560,580, 600, 620, 633,660, 700),labels =
c(500,540,560,580, 600, 620, 633,660, 700),cex.axis=0.7, cex.lab=0.8)
polygon(cord.x,cord.y,col='wheat4')
abline(v=633, col="steelblue4", lty=2, lwd=2)
text(600, 0.001, expression(mu))
text(660, 0.005, expression(paste("EI=", alpha, "=0.05")))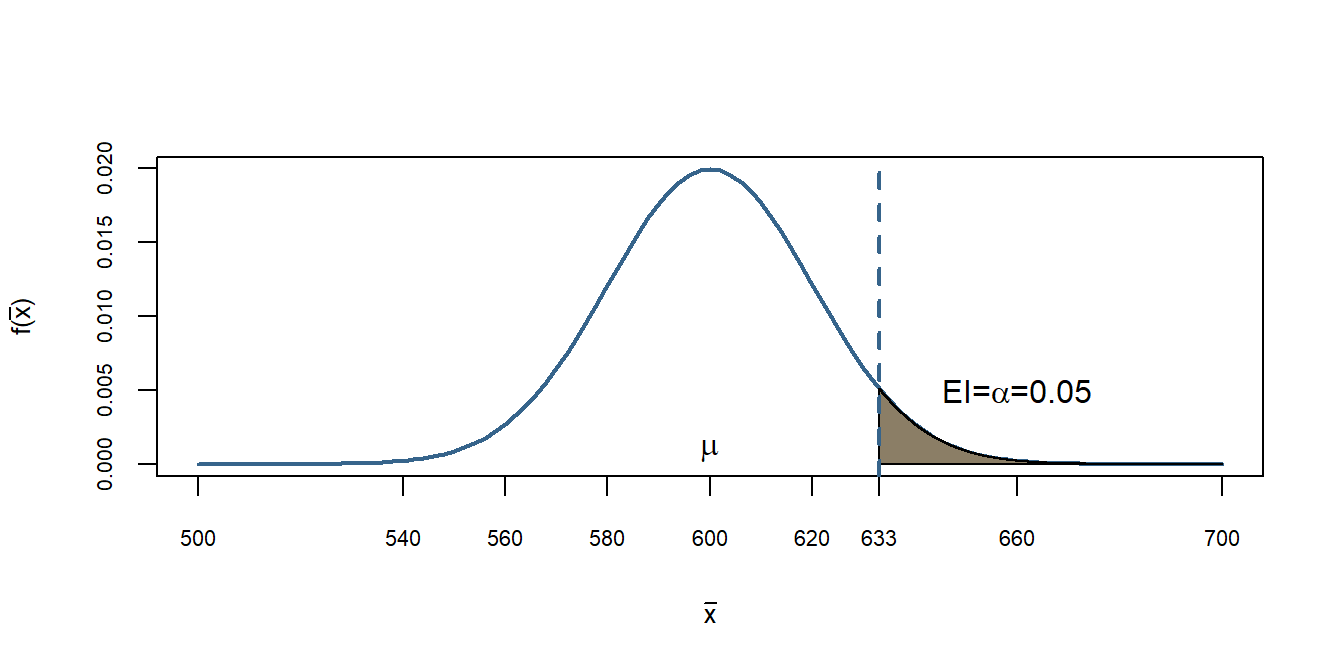
Em cinza tem-se a região crítica descrita acima. Logo todos os valores calculados de \(\bar{X}\) que cairem acima de 633, dizemos que rejeitamos \(H_0\). Entretanto, percebam que poderiam fazer parte desta distribuição, apesar da chance ser pequena, 5%.
Como não sabemos a distribuição sob \(H_1\) não conseguimos calcular a probabilidade de não rejeitar \(H_0\) e na verdade ela pertencer a distribuição de \(H_1\).
7.5.4 Procedimento Geral do Teste de Hipótese
7.5.4.1 Teste para um parâmetro populacional
Temos interesse em uma característica da população. Como vimos por exemplo, o tempo médio de um processo \(X\), ou mais especificamente na sua esperança \(E(X)=\mu\). Contruímos o teste sobre o parâmetro, podendo ser unicaudal ou bicaudal.
Hipótese Bicaudal:
O teste bilateral ou bicaudal podemos observar valores maiores ou menores em relação a hipótese nula. Assim não temos nenhum conhecimento que nos permita dizer que podemos ter valores somente maiores ou somente menores. Temos a seguinte formulação geral:
\[H_0: \qquad \theta=\theta_0\]
\[H_1: \qquad \theta \neq \theta_0\]
Nível de significância
Retomando o nosso exemplo, ao rejeitarmos \(H_0\) podemos cometer o erro de dizer que o tempo médio é maior que 600 dias, mas na realidade o tempo era efetivamente 600 dias.
Tentamos controlar esse tipo de erro que é o nosso Erro Tipo I (EI). Temos que definir qual seria o tamanho desse erro, 10%, 5%, 1% etc. Esse percentual é o que chamamos de nível de significância. Quem define esse tamanho é o pesquisador e em geral, em ciência sociais, utilizamos os níveis acima.
Nível de Significância:É a probabilidade máxima aceitável de cometer o erro tipo I e chamamos de \(\alpha\), sendo um valor entre \(0<\alpha<1\)
Dessa forma, faremos o teste de hipótese para o parâmetro \(\theta\) ao nível de significância de \(\alpha\). No nosso caso dizemos que iremos testar se o tempo médio dos processos é de 600, \(H_0: \mu=600\), ao nível de 5% de significância.
Valor Crítico e Região Crítica
Com base no nível de significância conseguiremos estabelecer qual é o valor crítico e qual seria a região de rejeição. Para o nosso caso encontramos o valor crítico de 633 e a nossa região foi estabelecida como \(RC =\{\bar{x} \in R | \bar{x} \geq 633\}\). Conforme calculamos anteiormente.
Assim, de forma geral tem-se:
\[RC =\{T \in C| H_0\}\] \[P(T \in C|H_0)\leq\alpha\]
A região critica depende do teste estatístico escolhido e se a hipótese é unilateral, ou seja, apenas de um lado da distribuição ou bilateral, os dois lados da distribuição. No caso unilateral utilizamos o nível de siginifcância, \(\alpha\), todo de um lado apenas. Se for o teste bilateral dividimos o nível de significância, ou seja, utilizamos\(\alpha /2\), metade para cada lado.
O Teste de Hipótese
Fazemos nosso processo de amostragem e obtemos o valor do teste estatístico. Se o valor do teste ficar fora da região crítica dizemos que não rejeitamos \(H_0\). Para o nosso caso, que não existe evidências de que o tempo médio dos processos é maior do 600 dias.
Caso o teste estatítico produza uma estimativa na região crítica, rejeitamos \(H_0\), há evidências de que o tempo médio é maior do que aquela postulada pela Justiça Federal.
7.5.5 Os Cinco passos para a contrução do teste de hipótese
- Estabeleça as hipótese nula \(H_0\) e a hipótese alternativa \(H_1\)
- Defina qual estimador do parâmetro populacional \(\theta\) que será usado para testar \(H_0\): média, desvio padrão amostral, proporção amostral etc
- Defina o nível de significância - \(\alpha\) e estabeleça qual o valor e a região crítica.
- Calcule a estimativa do teste estatístico.
- Se não pertencer a Região Crítica não rejeitamos \(H_0\), caso contrário rejeitamos a hipótese nula \(H_0\).
7.5.6 Introdução ao Teste de Hipótese de Duas Populações (de Médias)
O teste de hipótese é uma técnica estatística fundamental usada para tomar decisões baseadas em evidências amostrais. O teste de hipótese de duas populações é aplicado quando queremos comparar as médias de duas populações distintas e determinar se existe uma diferença estatisticamente significativa entre elas. Vamos explorar os principais conceitos deste teste:
Formulação das Hipóteses
No teste de hipótese de duas populações, formulamos duas hipóteses:
- Hipótese Nula (\(H_0\)): Esta é a hipótese inicial que assume que não há diferença entre as médias das duas populações. Geralmente, é representada como
\[H_0: \mu_1 = \mu_2\],
onde \(\mu_1\) e \(\mu_2\) são as médias das duas populações.
- Hipótese Alternativa (\(H_a\) ou \(H_1\)): Esta é a hipótese que queremos testar, indicando que há uma diferença significativa entre as médias das duas populações. Pode ser definida como: \[H_a: \mu_1 > \mu_2\] ou \[H_a: \mu_1 < \mu_2\] ou
\[H_a: \mu_1 \neq \mu_2\].
Estatística do Teste
O teste de hipótese de duas populações geralmente envolve o cálculo de uma estatística de teste específica para comparar as médias das amostras das duas populações. Uma das estatísticas comuns é o teste t de Student, especialmente quando as variâncias populacionais são desconhecidas e podem ser diferentes entre as populações.
Decisão do Teste
Após calcular a estatística de teste, comparamos o valor observado da estatística com um valor crítico ou calculamos um valor p associado. O valor p é a probabilidade de obter uma estatística de teste tão extrema quanto a observada, assumindo que a hipótese nula seja verdadeira. Com base no valor p (geralmente comparado com um nível de significância pré-definido, como 0,05), tomamos uma decisão de rejeitar ou não rejeitar a hipótese nula.
Conclusão do Teste
A conclusão do teste de hipótese de duas populações nos permite determinar se há evidências estatísticas suficientes para rejeitar a hipótese nula em favor da hipótese alternativa. Essa decisão tem implicações importantes em áreas como pesquisa científica, análise de dados e tomada de decisões em negócios e saúde.
7.5.7 Aplicação Prática sobre Teste de Hipótese
Essa seção tem o objetivo de aplicar o Teste de Hipótese utilizando o R. Vamos utilizar nosso banco de dados sobre feminicídio. E vamos criar uma variável que identifica se pertence as regiões norte, nordeste e centro oeste ou as regiões sul e sudeste.
#carregando o pacote para ler arquivos em excel
load("C:/Users/Alexandre_Nicolella/Aulas/FEA-RP/Jurimetria/jurimetria/final_fem_22.Rdata")
# Criando a Binária que indica a região N, NE e CO
library(dplyr)
final_fem_22 <- final_fem_22 %>%
mutate(N_NE_CO = case_when(
regiao %in% c("N", "NE", "CO") ~ 1, # Regiões N, NE e CO recebem 1
TRUE ~ 0 # Demais regiões recebem 0
))Vamos olhar as médias entra as regiões norte, nordeste e centro oeste e as regiões sul e sudeste.
library(kableExtra)
mean_1<- aggregate(final_fem_22[4:15], list(final_fem_22$N_NE_CO), mean, na.rm=T)
t(mean_1) %>%
kbl(digits = 2) %>%
kable_styling()| Group.1 | 0.00 | 1.00 |
| homic_abs | 249.71 | 108.80 |
| homic_tx | 3.60 | 5.18 |
| feminic_abs | 107.57 | 34.20 |
| feminic_tx | 1.47 | 1.72 |
| part_feminic | 42.84 | 35.98 |
| rendapc | 1903.14 | 1287.55 |
| mais_50 | 0.29 | 0.25 |
| t_homic_abs | 453.57 | 224.25 |
| t_homic_tx | 8.91 | 15.50 |
| t_feminic_abs | 177.67 | 78.79 |
| t_feminic_tx | 3.25 | 4.42 |
| part_t_feminic | 26.24 | 27.09 |
Pode-se observar que existem em todas as variáveis existem diferenças entre as duas regiões. A questão é: Essas diferenças são estatisticamente significativas?
Aproveitando um gráfico anterior que fizemos, vamos olhar a distribuição das taxas de feminicídio entre as regiões.
library(ggplot2)
ggplot(final_fem_22, aes(x = factor(N_NE_CO, labels = c("Sul e Sudeste", "Norte, Nord. e C.Oeste")), # Transformando em fatores
y = feminic_tx, fill = factor(N_NE_CO))) + # Taxa de Feminicídio por Fator
geom_violin(trim = FALSE, color = "white") + # Cria o gráfico de violino
scale_fill_manual(values = c("lightblue", "steelblue")) + # Cor das violas
stat_summary(fun="median", geom = "point", shape=19, size=3, color="darkorange" ) + # Vamos colocar o ponto mediana
labs(
title = "Distribuição da taxa de feminicídio por região do Brasil",
x = "Região",
y = "Taxa de Feminicídio (por 100 mil)",
fill = "Região"
) +
theme_minimal() +
theme(
plot.title = element_text(hjust = 0.5, size = 14, face = "bold"), # Centraliza o título
axis.text.x = element_text(size = 12), # Ajusta o tamanho dos rótulos no eixo X
axis.text.y = element_text(size = 10), # Ajusta o tamanho dos rótulos no eixo Y
legend.position = "none" )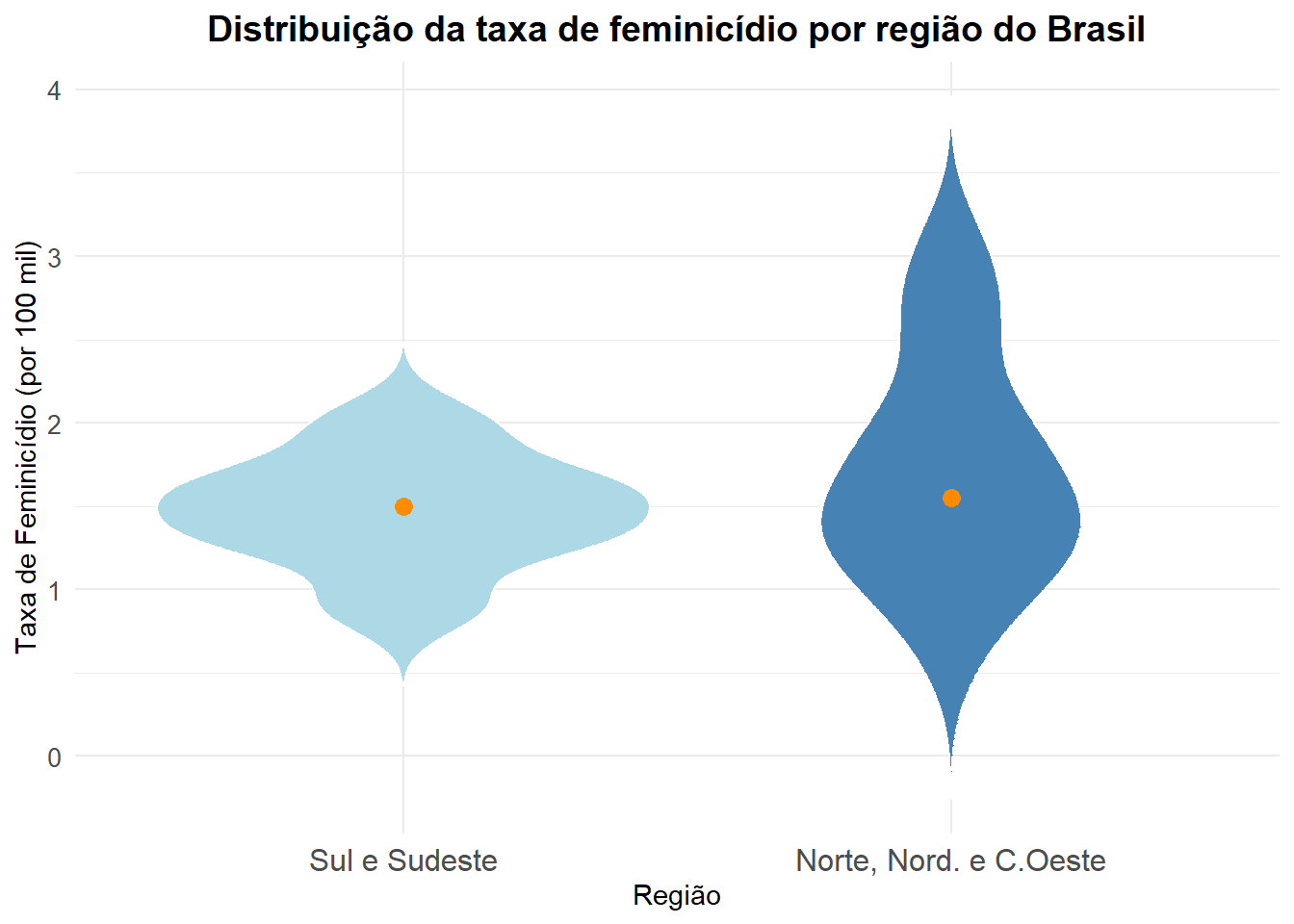
Observa-se diferença entre as duas regiões, mas será que as médias são estatisticamente diferentes? Para isso temos que utilizar o Teste de Hipótese.
Relembrando os Passos
O teste de hipótese segue um processo estruturado de cinco etapas:
Definir as Hipóteses – Comece formulando a hipótese nula (\(H_0\)) e a hipótese alternativa (\(H_1\)). Em geral, a hipótese nula representa a ausência de efeito ou diferença, enquanto a hipótese alternativa sugere a existência de um efeito ou diferença.
Defina o Estimador - Defina qual estimador vai utilizar para inferir sobre o parâmetro populacional \(\theta\), o qual será usado para testar \(H_0\): média, desvio padrão amostral, proporção amostral etc
Estabelecer os Critérios de Decisão – Defina o nível de significância (\(\alpha\)), que representa a probabilidade de rejeitar a hipótese nula quando ela é verdadeira (Erro Tipo I). Valores comuns de (\(\alpha\)) são 0,05 (5%) e 0,01 (1%).
Analisar os Dados da Amostra – Calcule o teste estatístico com base nos dados amostrais. Esse teste estatístico vai ser utilizado para a comparação com os valores típicos que poderiam acontecer se a amostra tivesse vindo de \(H_0\).
Tomar uma Decisão e Interpretar os Resultados – Compare o valor calculado no teste com o valor crítico ou utilize o p-valor. Se o p-valor for menor que o nível de significância \(\alpha\), rejeita-se a hipótese nula em favor da hipótese alternativa. Caso contrário, não há evidências suficientes para rejeitar a hipótese nula, indicando que o efeito não é estatisticamente significativo.
Teste de Hipótese no R
A função t.test() no R possui vários argumentos importantes para a realização do teste t.
t.test(x, y = NULL,
alternative = c("two.sided", "less", "greater"),
mu = 0, paired = FALSE, var.equal = FALSE,
conf.level = 0.95, …)Abaixo estão os principais:
x,y: As duas amostras de dados a serem comparadas.
alternative: Define a hipótese alternativa do teste (exemplo:"two.sided","greater","less").
mu: Especifica um valor de referência para a média populacional no teste.
paired: Indica se o teste t deve ser pareado (TRUE) ou não pareado (FALSE).
var.equal: Especifica se as variâncias das amostras devem ser assumidas como iguais (TRUE) ou não (FALSE).
conf.level: Define o nível de confiança do intervalo (padrão de 95%).
Esses parâmetros permitem personalizar o teste conforme a necessidade da análise estatística.
Teste sobre o Parâmetro
Uma reportagem em um portal de notícias indicou que a média da taxa de feminicídio nos estados brasileiros é igual a 2 assassinatos por 100 mil mulheres. Com base nos dados que coletamos gostaríamos de saber se eles carregam evidências favoráveis ou contra ao artigo.
- Definir as Hipóteses
\[H_0: \mu = 2\] \[H_1:\mu \neq 2 \]
- Defina o Estimador
Vamos utilizar a Média Amostral, \(\bar{X}\), para testar a hipótese nula \(H_0\).
- Estabelecer os Critérios de Decisão
Vamos adotar \(\alpha= 0,05\) (5%).
- Analisar os Dados da Amostra
t.test(x=final_fem_22$feminic_tx, y = NULL,
alternative = c("two.sided"),
mu = 2,
paired = FALSE,
var.equal = TRUE,
conf.level = 0.95)
One Sample t-test
data: final_fem_22$feminic_tx
t = -2.9276, df = 26, p-value = 0.007011
alternative hypothesis: true mean is not equal to 2
95 percent confidence interval:
1.407411 1.896292
sample estimates:
mean of x
1.651852 - Tomar uma Decisão e Interpretar os Resultados
Entendendo o resultado do teste:
One Sample t-test: Teste de uma amostra -> taxa de feminicídio
data: final_fem_22$feminic_tx: Indica a variável que utilizou
t = -2.9276, df = 26, p-value = 0.007011: O valor do teste t, o grau de liberdade e o p-valor
alternative hypothesis: true mean is not equal to 2: A hipótese alternativa é que a média não é igual a 2
95 percent confidence interval: 1.407411 1.896292 : O intervalo de confiança de 95% para a média, indicando que a verdadeira média populacional está nesse intervalo.
sample estimates: mean of x = 1.651852: A média amostral é de 1.65, a qual é a estimativa da verdadeira média populacional.
Como o p-valor foi menor que o nível de significância \(\alpha\), rejeita-se a hipótese nula em favor da hipótese alternativa. Há evidências de que a média nacional é menor do que 2.
Teste Unicaudal
Podemos testar também a seguinte hipótese com nível de significância de 1%:
\[H_0: \mu = 2\] \[H_1:\mu < 2 \] No R:
t.test(x=final_fem_22$feminic_tx, y = NULL,
alternative = c("less"),
mu = 2,
paired = FALSE,
var.equal = TRUE,
conf.level = 0.99)
One Sample t-test
data: final_fem_22$feminic_tx
t = -2.9276, df = 26, p-value = 0.003505
alternative hypothesis: true mean is less than 2
99 percent confidence interval:
-Inf 1.946607
sample estimates:
mean of x
1.651852 Novamente como o p-valor foi menor que o nível de significância \(\alpha\), rejeita-se a hipótese nula em favor da hipótese alternativa. Há evidências de que a média nacional é menor do que 2.
Teste para Diferença de Médias
- Taxa de Feminicídio
Vamos testar a hipótese de que as taxas de feminicídio são iguais entre as regiões norte, nordeste e centro oeste e as regiões sul e sudeste. Vamos permitir que as variâncias sejam diferentes entre as duas regiões
\[H_0: \mu_{N-NE-CO} = \mu_{S-SD}\] \[H_1: \mu_{N-NE-CO} \neq \mu_{S-SD}\]
t.test(feminic_tx~N_NE_CO, data=final_fem_22,
alternative = c("two.sided"),
var.equal = FALSE,
conf.level = 0.95)
Welch Two Sample t-test
data: feminic_tx by N_NE_CO
t = -1.2049, df = 20.949, p-value = 0.2417
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
-0.6640345 0.1768916
sample estimates:
mean in group 0 mean in group 1
1.471429 1.715000 Como o p-valor foi maior que o nível de significância \(\alpha\), não rejeita-se a hipótese nula. Não há evidências de que as regiões possuem taxas diferentes de feminicídio.
- Renda pc
Vejamos agora a renda per capita a 1% de significância :
t.test(rendapc~N_NE_CO, data=final_fem_22,
alternative = c("two.sided"),
var.equal = FALSE,
conf.level = 0.99)
Welch Two Sample t-test
data: rendapc by N_NE_CO
t = 4.6401, df = 22.301, p-value = 0.0001225
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
99 percent confidence interval:
242.1018 989.0840
sample estimates:
mean in group 0 mean in group 1
1903.143 1287.550 Observa-se que rejeita-se a hipótese nula, e há evidências de que a média da renda per capita entre as duas regiões são diferentes.
Amostras Pareada
Vamos testar a diferença de média entre amostra pareadas. A amostra pareada é quando temos o mesmo indivíduo observado duas vezes. Vamos testar se existe diferença entre a participação do feminicídio sobre os homicídios e a participação da tentativa de feminicídio sobre as tentativas de feminicídio feminino.
\[H_0: \mu_{part-feminic} = \mu_{part-t-feminic}\] \[H_1: \mu_{part-feminic} \neq \mu_{part-t-feminic}\]
Utilizando a média amostral para testar a hipótese nula \(H_0\) e considerando um nível de significância de 95%. No R temos:
t.test(x=final_fem_22$part_feminic, y=final_fem_22$part_t_feminic,
alternative = c("two.sided"),
paired = TRUE,
var.equal = FALSE,
conf.level = 0.95)
Paired t-test
data: final_fem_22$part_feminic and final_fem_22$part_t_feminic
t = 3.457, df = 24, p-value = 0.002049
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
4.105405 16.269795
sample estimates:
mean difference
10.1876 Como o p-valor foi menor que o nível de significância \(\alpha\), rejeita-se a hipótese nula em favor da hipótese alternativa. Há evidências de que a média da participação do feminicídio é maior do que a média da participação da tentativa de feminicídio. A estimativa dessa diferença é de 10 pontos percentuais a mais para participação do feminicídio.

